icode
iqqcode
2021-06-17
目录

约瑟夫环

# 1. 约瑟夫环问题

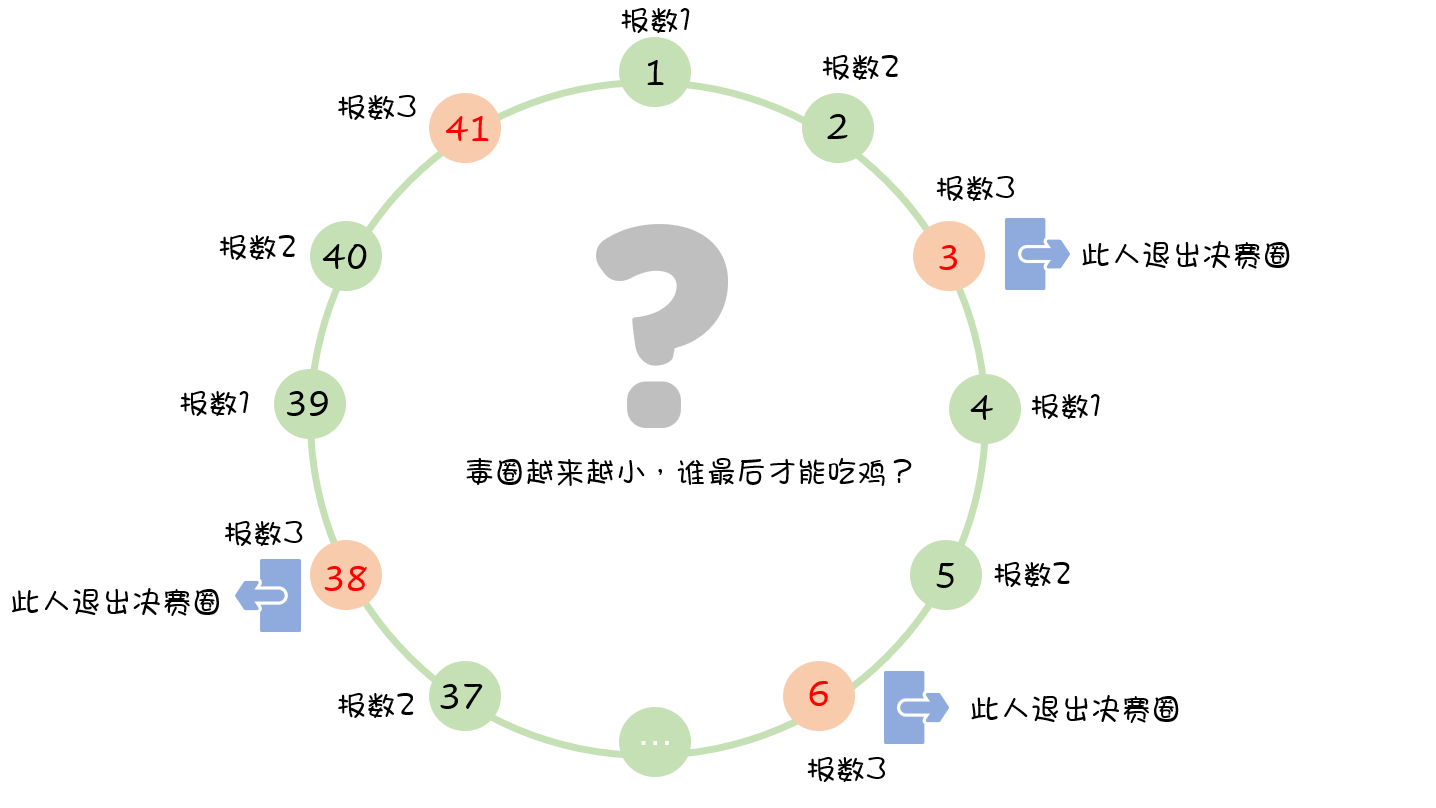
传说有这样一个故事，在罗马人占领乔塔帕特后，39 个犹太人与约瑟夫及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，第一个人从1开始报数，依次往后，如果有人报数到3，那么这个人就必须自杀，然后再由他的下一个人重新从1开始报数，直到所有人都自杀身亡为止。然而约瑟夫和他的朋友并不想遵从。于是，约瑟夫要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，从而逃过了这场死亡游戏 。

问题转换：

n个人坐一圈，第一个人编号为1，第二个人编号为2，第n个人编号为n。

  1. 编号为1的人开始从1报数，依次向后，报数为ans的那个人退出圈；

  2. 自退出那个人开始的下一个人再次从1开始报数，以此类推；

  3. 求出最后退出的那个人的编号

看来，约瑟夫是玩过双排，知道决赛圈怎么打，才能带基友吃鸡。一跳飞机别人都在唯唯诺诺，约瑟夫同志直接规划好在决赛圈躺赢。

现在，我来告诉你当年约瑟夫是怎么想的，怎么用以下方法直接在决赛圈躺赢吃鸡！

说来惭愧，作为一个大三的老菜鸡，数据结构我在大一学过了，但是当时觉得这玩意好复杂，感觉没啥用，就上课划水。但是，比较有印象的一节课就是老师讲约瑟夫环问题，当时也没怎么搞懂，现在重头来。如果有刚接触开始学习数据结构的同学，一定要好好学习呀。

# 2. 分析一波

约瑟夫问题是个环，我们把每个人编号后放到这个环中。首先，这个环怎么来实现呢？数据结构里也没有环呀？

我们首先想到的应该就是循环链表，这是个环呀。那，链表能实现的，数据应该也可以呀。

其实，约瑟夫环问题共有三种解法，分别是循环链表，数组，还有数学方法来解决。

# 循环链表

【循环链表解题思路】：

  1. 构建含有n个结点的单向循环链表，分别存储1~n的值，分别代表这n个人；

  2. 使用计数器count，记录当前报数的值；

  3. 遍历链表，每循环一次，count++；

  4. 判断count的值，如果是ans，则从链表中删除这个结点并打印结点的值，把count重置为0；

来具体分析一下链表解题思路是怎么做的？

首先是来构建节点数为n的循环链表

  • 创建节点类

  • 构建循环链表

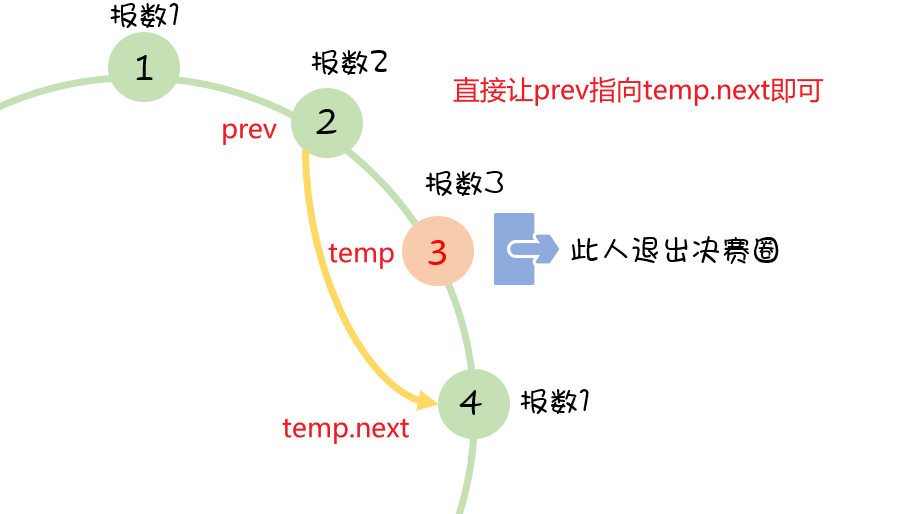
其次是开始循环报数，删除节点

删除节点的细节性操作：

【完整的代码】

package com.topic.joseph;

/**
 * @Author: Mr.Q
 * @Date: 2020-05-06 21:10
 * @Description:循环链表
 * @Solution:
 * 1.构建含有41个结点的单向循环链表，分别存储1~41的值，分别代表这41个人；
 * 2.使用计数器count，记录当前报数的值；
 * 3.遍历链表，每循环一次，count++；
 * 4.判断count的值，如果是3，则从链表中删除这个结点并打印结点的值，把count重置为0
 */
public class CircularList {
    /**
     * 约瑟夫环
     * @param n 围成环人的编号(从1开始到n)
     * @param ans 数到ans的那个人出列
     * @return 幸存人的编号
     */
    public static int joseph(int n, int ans) {
        if ( ans < 2) {
            return n;
        }
        //创建循环链表
        Node first = buildCircularList(n);

        //count计数器，模拟报数
        int count = 0;

        //遍历删除节点，模拟自杀
        //记录每次遍历(报数)拿到的节点
        Node<Integer> temp = first;
        //记录当前节点的上一个节点befo，为的是在删除(自杀)时，befo直接指向自杀节点的下一个节点，完成当前节点的删除
        Node<Integer> befo = null; //默认的首节点无上一个节点

        //如果当前环只剩最后一个节点时，结束循环(防止自环)
        while (temp != temp.next) {
            //模拟报数
            count++;
            //判断当前报数是不是ans
            if (count == ans) {
                //如果是ans，则把当前结点删除调用，打印当前结点;
                //重置count=0，让当前结点temp后移
                befo.next = temp.next; //befo直接指向自杀节点的下一个节点，完成当前节点的删除
                System.out.print(temp.data + " ");
                count = 0;
                temp = temp.next;
            }else {
                //如果不是ans，让befo变为当前结点，让当前结点后移
                befo = temp;
                temp = temp.next;
            }
        }
        return temp.data;
    }

    //节点类
    private static class Node<T> {
        //存储数据
        T data;
        //指向下一个节点
        Node next;
        public Node(T data, Node next) {
            this.data = data;
            this.next = next;
        }
    }

    /**
     * 构建循环链表,分别存储1~n的编号
     * @param n n人编号
     * @return
     */
    private static Node buildCircularList(int n) {
        //首节点构建
        Node<Integer> first = null;
        //记录新创建的节点的前一个节点prev
        Node<Integer> prev = null;
        for (int i = 1; i <= n; i++) {
            //如果是第一个节点
            if (i == 1) {
                //首节点放入编号1，指向为空(因为此时后面还没有节点，链表只有一个节点)
                first = new Node<> (i, null);
                prev = first;
                continue; //本次循环执行结束
            }

            //如果不是第一个节点,将产生的新节点链在prev后
            Node<Integer> node = new Node<> (i, null);
            prev.next = node;
            //链接之后，让prev指向当前链表的最新节点，继续创建下一个新节点
            prev = node;

            //如果是最后一个节点，则需要指向first，形成循环链表
            if (i == n) {
                prev.next = first;
            }
        }
        return first;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101

# 数组

数组的思想就是通过一个数组，数组中每个元素都是一个人，然后对数组进行循环处理，反复遍历来达到”环“的效果，每当数组中的人数到ans时，将其标记为淘汰。直到最后数组中只有一个人未被淘汰。

为了更直观的体现淘汰与存货两种状态，我们创建一个boolean数组。

当然，int数组也可以，把数组按1-n编号，只需要把淘汰的元素致为-1即可。boolean类型的巧妙之处就是利用数组下标来编号。

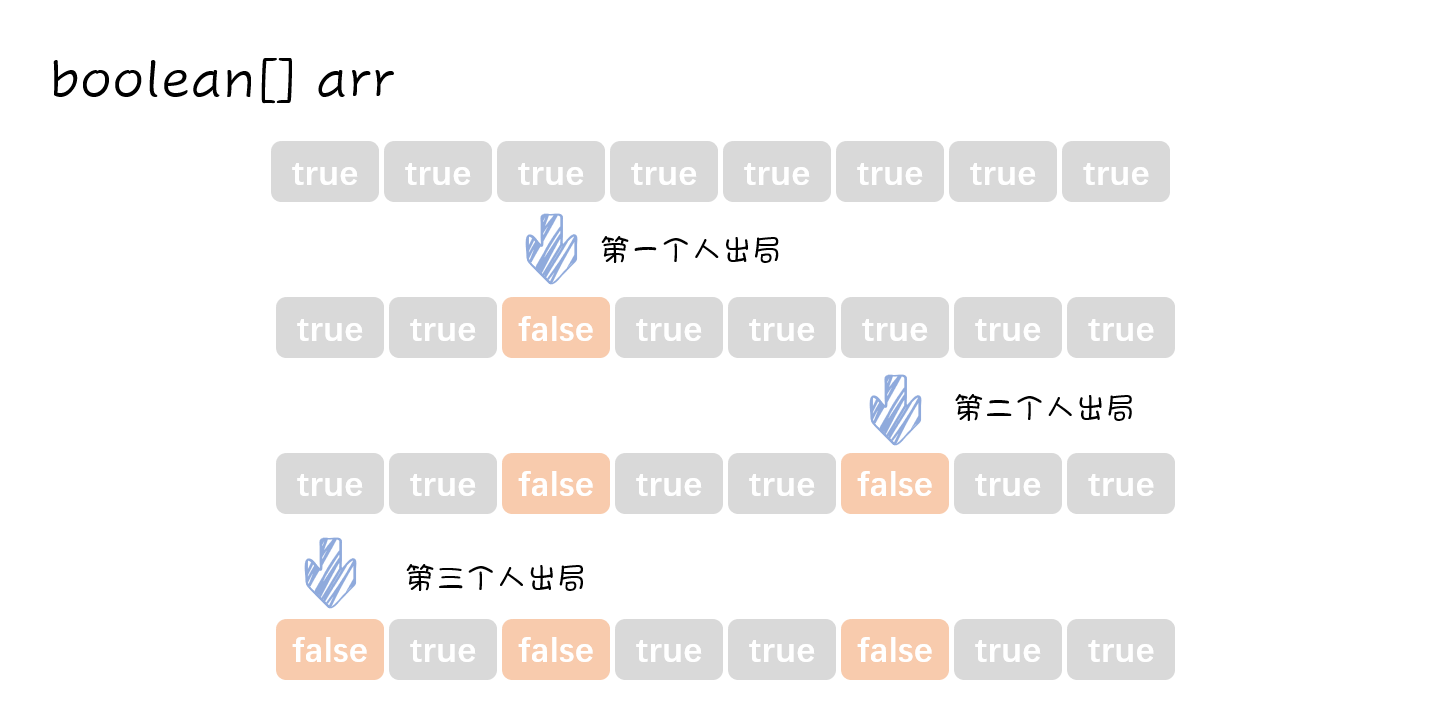
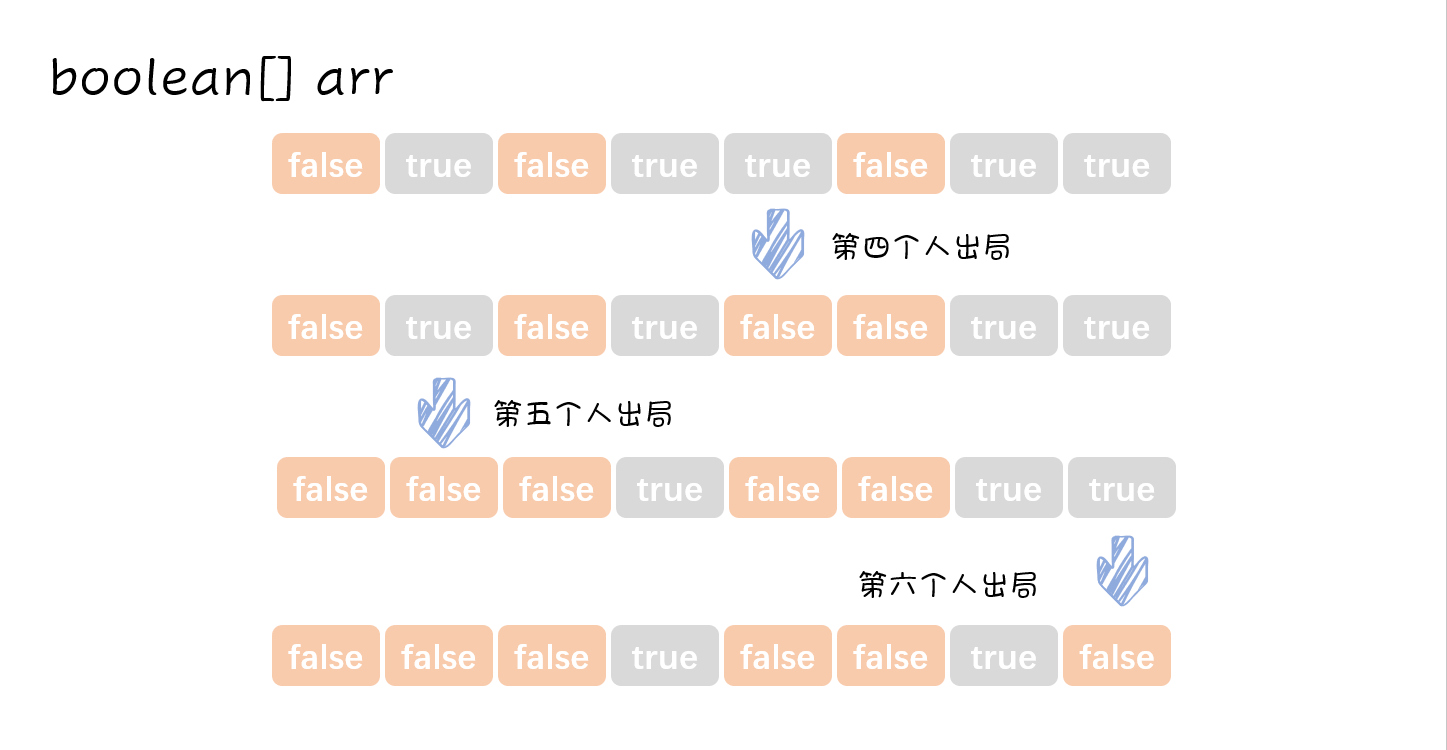
【第一步】我们需要一个长度为n的布尔值数组，数组的index就表示了第几个人，元素的true和false表示了这个人是否被淘汰。一开始我们需要将所有人都设置为未被淘汰。

【第二步】 我们需要三个变量：

  1. stay记录剩下未被淘汰的人数，初始值为总人数；

  2. count计数器，每过一个人加一，加到ans时归零，初始化为0

  3. index标记从哪里开始，index记录了此时数到了第几个人，当index等于总人数n时归零 ，初始化为0 因为是一个圈，所以最后一个人数完后又轮到第一个人数

【第三步】开始循环计算了

  • 首先判断剩余的人数是否大于一，如果大于一进入循环；

  • 判断第index人，如果这个人未被淘汰，则计数器加一，如果等于ans则淘汰这个人，否则跳过计数继续

  • 当index等于总人数n时，第二轮循环开始

【最后】计算结束后，数组中只有一个元素为true，而这个就是约瑟夫那位靓仔了！

【完整代码】

package com.topic.joseph;

/**
 * @Author: Mr.Q
 * @Date: 2020-05-07 09:12
 * @Description:数组求解
 * @Solution:
 */
public class ArraySolution {
    /**
     * @param n 围成环人的编号(从1开始到n)
     * @param ans 数到ans的那个人出列
     * @return 幸存人的编号
     */
    public static int joseph(int n, int ans) {
        //开始时设置一个长度为n的数组，并将元素都设为true
        //数组的下标代表人到编号，数组元素的值(T,F)代表是否淘汰
        Boolean[] peopleFlags = new Boolean[n];
        for (int i = 0; i < n; i++) {
            peopleFlags[i] = true;
        }

        //剩下未被淘汰的人数
        int stay = n;
        //计数器，每过一个人加一，加到ans时归零
        int count = 0;
        //标记从哪里开始，index记录了此时数到了第几个人，当index等于总人数n时归零
        //因为是一个圈，所以最后一个人数完后又轮到第一个人数
        int index = 0;
        while (stay > 1) {
            if (peopleFlags[index]) {
                //说明还没有被淘汰 计数器加1
                count++;
                if (count == ans) {
                    count = 0; //计数器归0
                    peopleFlags[index] = false; //此人被淘汰
                    stay--; //未被淘汰的人数-1
                }
            }
            index++;

            //数到本轮最后一人时，则又从第一人开始计数
            if (index == n) {
                index = 0;
            }
        }

        //经过上面的循环，现在数组中被淘汰的人都标记为false，最后没被淘汰都人标记为true
        for (int j = 0; j < n; j++) {
            if (peopleFlags[j]) {
                return j + 1;
            }
        }
        return -1;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

# 数学解法

这就涉及到咱的知识盲区了，作为一个数学渣渣，就算把头发拔光也想不出来。不过，咱学学大佬们怎么操作。

首先我们把这n个人的序号编号从0~n-1（理由很简单，由于m是可能大于n的，而当m大于等于n时，那么第一个出列的人编号是m%n，而m%n是可能等于0的，这样编号的话能够简化后续出列的过程）.

当数到m-1的那个人出列，因此我们编号完成之后，开始分析出列的过程：

第一次出列：

一开始的时候，所有人的编号排成序列的模式即为：

0, 1, 2, 3, 4, 5 ... n-2，n-1

那么第一次出列的人的编号则是(m-1)%n1，那么在第一个人出列之后，从他的下一个人又开始从0开始报数，为了方便我们设

k1 = m%n1（n1为当前序列的总人数）那么在第一个人出列之后，k1则是下一次新的编号序列的首位元素，

那么我们得到的新的编号序列为：

k1，k1+1，k1+2，k1+3...n-2，n-1，0，1，2...k1-3，k1-2 (k1-1第一次已出列)

那么在这个新的序列中，第一个人依旧是从0开始报数，那么在这个新的序列中，每个人报的相应数字为：

0, 1, 2, 3 .... n-2

那么第二次每个人报的相应数字与第一次时自己相应的编号对应起来的关系则为：

0 --> k1

1 --> k1+1

2 --> k1+2

...

n-2 ---> (k1+n-2)%n1(n1为当前序列的总人数，因为是循环的序列，k1+n-1可能大于总人数)

那么这时我们要解决的问题就是n-1个人的报数问题（即n-1阶约瑟夫环的问题）

可能以上过程你还是觉得不太清晰，那么我们重复以上过程，继续推导剩余的n-1个人的约瑟夫环的问题：

那么在这剩下的n-1个人中，我们也可以为了方便，将这n-1个人编号为：

0,1,2,3,4...n-2

那么此时出列的人的编号则是（m-1） % n2（n2为当前序列的总人数），同样的我们设k2 = m % n2，那么在这个人出列了以后，序列重排，重排后新的编号序列为：

k2，k2+1，k2+2，k2+3...n-2，n-1，0，1，2...k2-3，k2-2 (k2-1第一次已出列)

那么在这个新的序列中，第一个人依旧是从1开始报数，那么在这个新的序列中，每个人报的相应数字为：

1,2，3,4....n-2

那么这样的话是不是又把问题转化成了n-2阶约瑟夫环的问题呢？

后面的过程与前两次的过程一模一样，那么递归处理下去，直到最后只剩下一个人的时候，便可以直接得出结果 当我们得到一个人的时候（即一阶约瑟夫环问题）的结果，那么我们是否能通过一阶约瑟夫环问题的结果，推导出二阶约瑟夫环的结果呢？

借助上面的分析过程，我们知道，当在解决n阶约瑟夫环问题时，序号为k1的人出列后，剩下的n-1个人又重新组成了一个n-1阶的约瑟夫环，那么:

假如得到了这个n-1阶约瑟夫环问题的结果为ans（即最后一个出列的人编号为ans），那么我们通过上述分析过程，可以知道，n阶约瑟夫环的结果： (ans + k)%n(n为当前序列的总人数)，而k = m%n

则有：n阶约瑟夫环的结果

(ans + m % n)%n，那么我们还可以将该式进行一下简单的化简：

  • 当 m < n 时，易得上式可化简为：（ans + m）% n

  • 而当m>=n时，那么上式则化简为：（ans % n + m%n%n）% n 即为：（ans % n + m%n）% n

  • 而 （ans + m）% n = （ans % n + m%n）% n

因此得证：

(ans + m % n)%n = （ans + m）% n

这样的话，我们就得到了递推公式，由于编号是从0开始的，那么我们可以令

f[1] = 0;//当一个人的时候，出队人员编号为0

f[n] = (f[n-1] + m)%n; //m表示每次数到该数的人出列，n表示当前序列的总人数

而我们只需要得到第n次出列的结果即可，那么不需要另外声明数组保存数据，只需要直接一个for循环求得n阶约瑟夫环问题的结果即可

由于往往现实生活中编号是从1-n，那么我们把最后的结果加1即可

果然啊，数学才是大哥。

# 使用Java提供的LinkedList

相比较于自己实现的循环链表，用API的LinkedList简化了很多，关键是在于remove()方法。

  • 设置index指针，模拟报数。到达ans或者一轮判断走完时重置

  • remove删除自杀的节点，来不断缩短链表长度

  • 最终链表只剩一个元素，即为存活的约瑟夫的编号

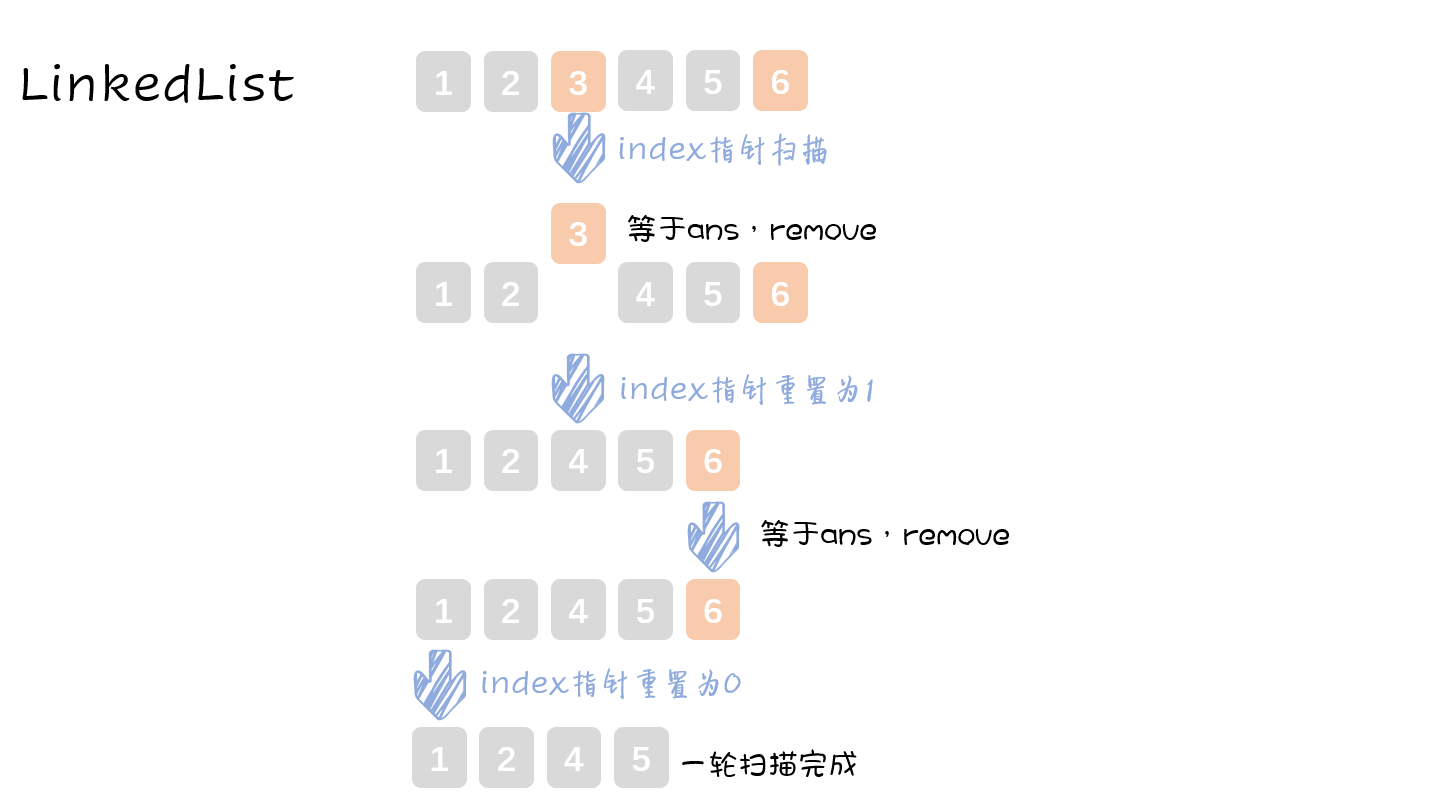
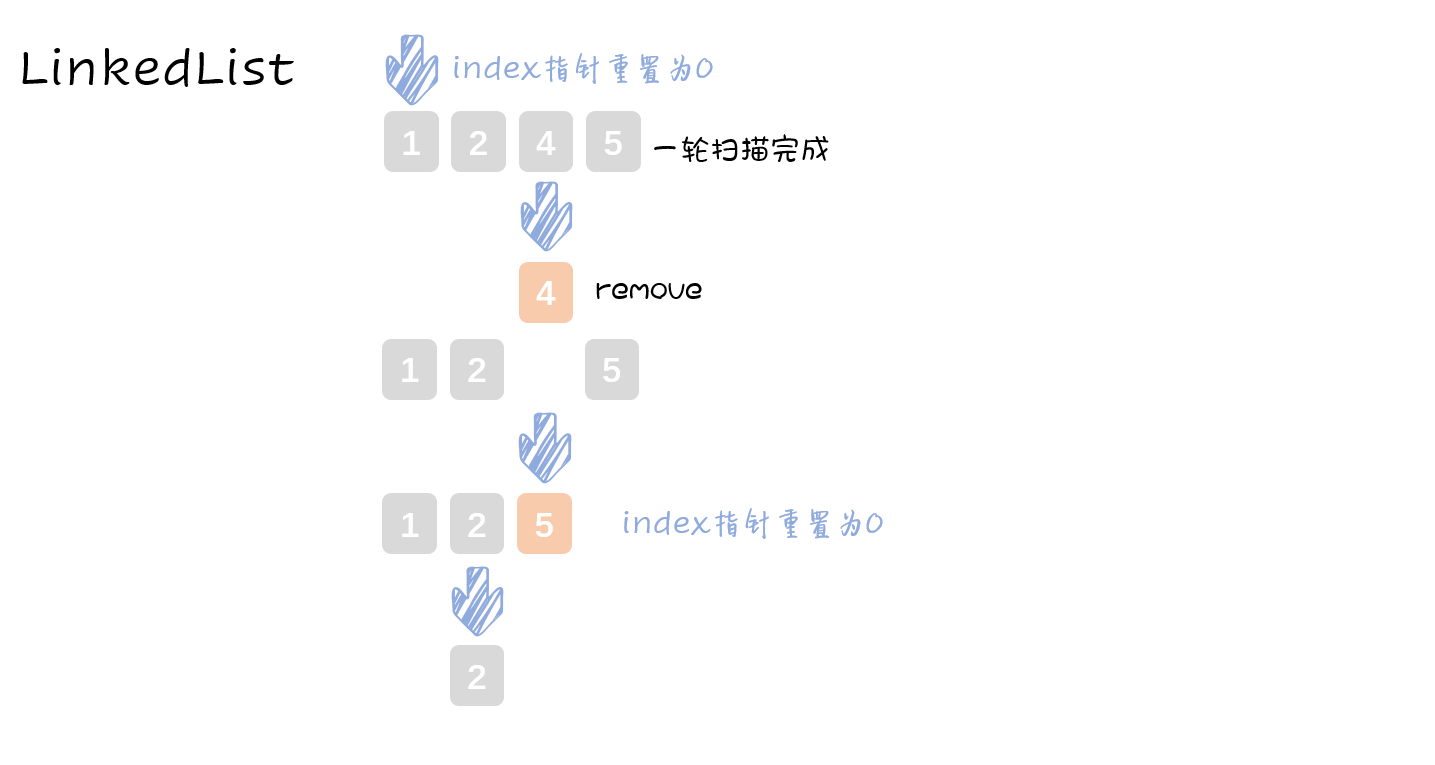
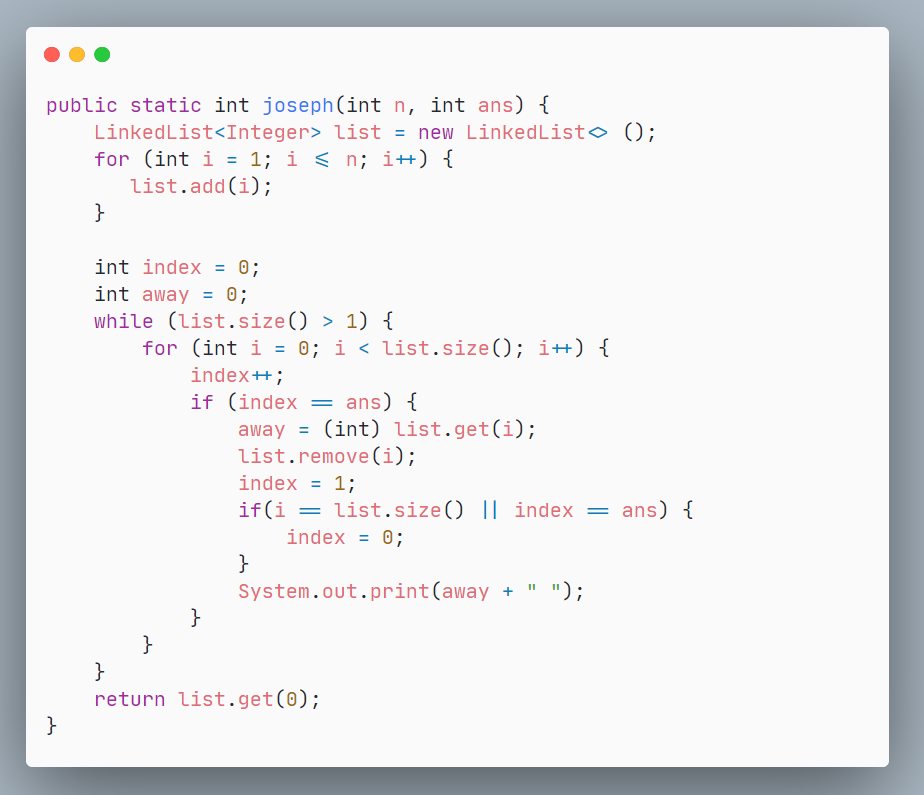
【代码】

/**

 * @Author: Mr.Q
 * @Date: 2020-05-08 18:26
 * @Description:Java自带链表实现
 */
public class LinkedListSolution {
    public static int joseph(int n, int ans) {
        LinkedList<Integer> list = new LinkedList<> ();
        for (int i = 1; i <= n; i++) {
           list.add(i);
        }
        int index = 0;
        while (list.size() > 1) {
            for (int i = 0; i < list.size(); i++) {
                index++;
                int away = 0;
                if (index == ans) {
                    away = list.get(i);
                    list.remove(i);
                    index = 1;  //指针重置
                    if(i == list.size() || index == ans){
                        index = 0;
                    }
                    System.out.print(away + " ");
                }
            }
        }
        return list.get(0);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

这不就简简单单奥利干了么，当年的约瑟夫，就是这么躺赢的！

【参考文章】

  1. 约瑟夫环问题 (opens new window)

  2. 约瑟夫环的几种实现方式 (opens new window)

  3. 使用JAVALinkedList解决约瑟夫圆环问题 (opens new window)

编辑 (opens new window)
上次更新: 2021/08/07, 16:45:58
SpringBoot经典学习笔记
单例模式

← 单例模式→

最近更新
01
匿名内部类
10-08
02
函数式接口
10-08
03
ARouter-Kotlin踩坑
10-05
更多文章>
Theme by Vdoing | Copyright © 2021-2023 iqqcode | MIT License | 备案号-京ICP备2021028793号
×