快速排序
# 1. 快速排序思想
快速排序（Quick_Sort)基于分治算法实现
它的基本思想是：
- 选择一个基准数（就是以它作为参考数），通过一趟排序这个基准数将要排序的一组数分割成==两个部分==；基准数就像一个中间的标签，分成的两个子序列，一部分比它大，一部分比它小。
- 通过分治的思想（化解为子问题，递归调用），对两个子序列再分别进行快速排序，而中间的标签位置固定好之后就不再发生改变。以此达到整个数据变成有序的序列。
快速排序流程：
【动图详解】
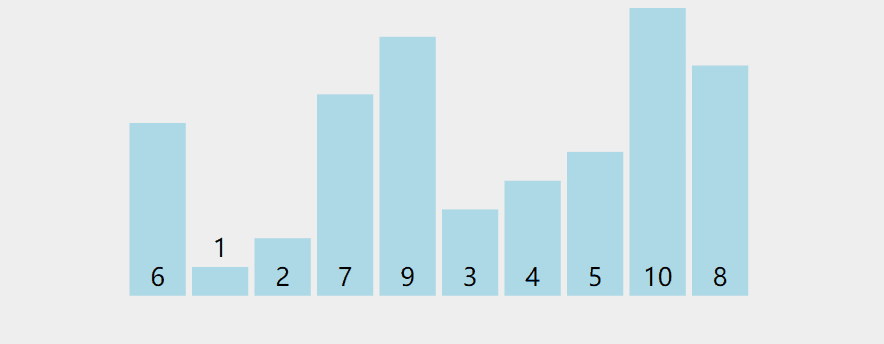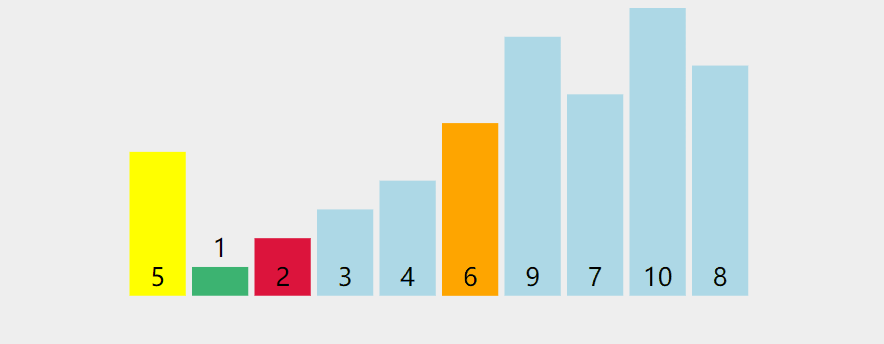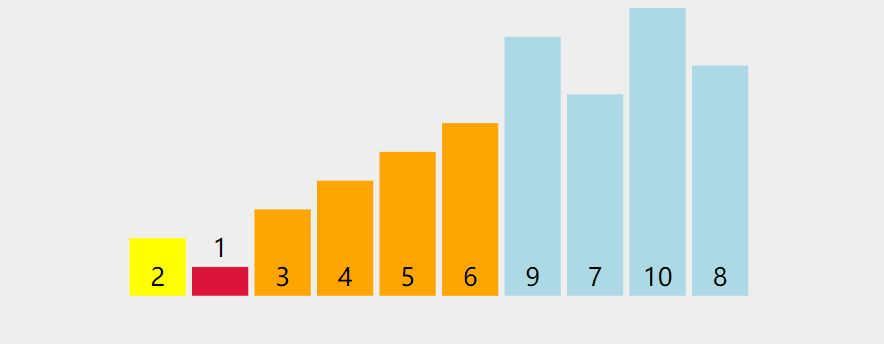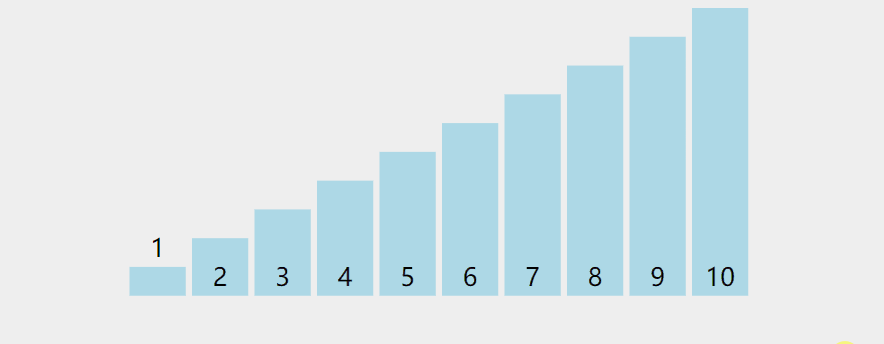
# 2. 快速详解
现在我们要对下面序列进行从左到右由小到大的排序
在初始状态下，数字6在序列的第1位。我们的目标是将6挪到序列中间的某个位置，假设这个位置是k。现在就需要寻找这个k，并且以第k位为分界点，左边的数都小于等于6，右边的数都大于等于6。想一想，你有办法可以做到这点吗？
我们可以联想到冒泡排序，依次和相邻的数进行比较，直到让6到达中间的分界点；但这样每次只能移动一个数，效率相对低下而复杂。怎样才能让6快速到达中间的位置呢？我们引入哨兵思想！
哨兵思想：
[ ] 引入哨兵 i ， j，分别放在数列的队头和队尾；
[ ] 让哨兵 i 指向队头元素，让哨兵 j 指向队尾一个元素；
i ，j 哨兵分别从初始序列 “6 1 2 7 9 3 4 5 10 8” 两端开始 “探测”
j 先从右往左找一个小于6的数，i 再从左往右找一个大于6的数，然后交换他们。
刚开始的时候让哨兵 i 指向序列的最左边（即 i=1），指向数字6。让哨兵j指向序列的最右边（即 j=10），指向数字8
首先哨兵 j 开始出动。因为此处设置的基准数是最左边的数，所以需要让哨兵j先出动，这一点非常重要。哨兵j一步一步地向左挪动（即 j- -），直到找到一个小于6的数停下来。
接下来哨兵i再一步一步向右挪动（即 i++），直到找到一个数大于6的数停下来。最后哨兵j停在了数字5面前，哨兵i停在了数字7面前
哨兵 i 从左向右找大于基准数的数，哨兵 j 从右向左找小于基准数的数
双方哨兵找到了目标，然后交换目标
接下来开始哨兵 j 继续向左挪动（每次必须是哨兵 j 先出发），哨兵 j 赶往下一个位置，指向4，再次发现目标；通知 i 哨兵行动
哨兵i也继续向右挪动的，他发现了9（比基准数6要大，满足要求）之后停了下来，继续交换
哨兵 j 继续向左挪动，他发现了3（比基准数6要小，满足要求）之后又停了下来。
哨兵 i 继续向右移动，糟啦！此时哨兵i和哨兵 j 相遇了（确认过眼神，好鸡冻），哨兵 i 和哨兵 j 都走到3面前。说明此时“探测”结束,每次俩人相遇时，探测结束。
此时，哨兵 i 和 j 所指向的位置，就是我们要找的分界点 k 
现在基准数6已经归位，它正好处在序列的第6位。此时以基准数6为分界点，6左边的数都小于等于6，6右边的数都大于等于6。
回顾一下刚才的过程，其实哨兵 j 的使命就是要找小于基准数的数，而哨兵 i 的使命就是要找大于基准数的数，直到 i 和 j 碰头为止。
到此，第一次交换结束。可以大体上将数分为大于基准数和小于基准数两组。
接下来还需要分别处理这两个子序列。因为6左边和右边的序列目前都还是很混乱的。不过不要紧，我们已经掌握了方法，接下来只要模拟刚才的方法分别处理6左边和右边的序列即可。
处理6左边的序列，6的位置就固定不动了 
j 哨兵向左寻找比基准数3小的数，它发现了2；
i 哨兵开始出发。但是，跨过了山和大海，穿过了人山人海，走过了3，路过了1，任然没有发现比 3 大的数，只能空手和 j 哨兵哥哥相遇了
此时，3作为基准数，再次将数列分成2部分；然后又是两个子序列，分而治之
然后，哨兵 i， j对2 1，5 4再进行排序，3的位置固定不动；
对序列 2 1 以2为基准数进行调整，序列1只有一个数，直接将2和1交换位置即可。处理完毕之后的序列为1 2，到此2已经归位。
序列5 4的处理也仿照此方法，最后得到的序列如下：
以6为基准数的序列左面排序完成
对于序列9 7 10 8也模拟刚才的过程，直到不可拆分出新的子序列为止。最终将会得到这样的序列:
# 3. 代码实现
版本一
public void quickSort(int[] arr, int low, int high) {
if (low < high) {
// 左边界基准数,由于是递归调用，此处为arr[low]，不能是arr[0]
int key = arr[low];
int i = low, j = high;
while (i < j) {
// j从右向左移动寻找，临界条件为 j == left，已经扫描到最左边了，无需继续扫描
while (i < j && arr[j] > key) {
// 先从右向左找第一个小于key的数
j--;
}
// 将左右找到的元素进行交换
if (i < j) arr[i++] = arr[j];
// i从左向右移动寻找，临界条件为 i == right，已经扫描到了最右边了，无需继续扫描
while (i < j && arr[i] < key) {
// 再从左向右找第一个大于key的数
i++;
}
if (i < j) arr[j--] = arr[i];
}
// 基准数归位
arr[i] = key;
//让左子组有序(退出循环的临界条件为 i == j)
quickSort(arr, low, i - 1);
//让右子组有序
quickSort(arr, i + 1, high);
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
【代码说明】
- 由于要交换元素，但是在数组中原地操作。所以
pivot充当临时变量temp，在交换中会有一个值被覆盖 - 被覆盖的值腾出空间来完成
arr[i]和arr[j]交换元素 arr[i] = key;最终还原回被覆盖的值
运行结果
QuickSort 排序结果为：[1, 2, 3, 4, 5, 5, 6, 7, 9, 10]
版本二 基准数方法独立
public class QuickSort {
public static void quick(int[] arr, int low, int high) {
if (low >= high) {
return;
}
//需要对数组中low索引到high索引处的元素进行分组（左子组和右子组）
//返回的是分组的分界值所在的索引，分界值位置变换后的索引
int pivot = partition(arr, low, high);
//递归调用让左子组有序
quick(arr, low, pivot - 1);
//让右子组有序
quick(arr, pivot + 1, high);
}
/**
* 对数组a中，从索引low到索引high之间的元素进行分组，并返回分组界限对应的索引
*/
public static int partition(int[] arr, int low, int high) {
int key = arr[low];
int i = low, j = high;
while (i < j) {
// 先从右向左找第一个小于key的数
while (i < j && arr[j] > key) {
j--;
}
// 再从左向右找第一个大于等于key的数(切记加上=)
while (i < j && arr[i] <= key) {
i++;
}
//交换 i和 j指针所指向的元素
if (i < j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
//key和指针重合点交换
arr[low] = arr[i];
arr[i] = key;
// i == j
return i;
}
public void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
【代码参考】
运行结果
QuickSortMethod 排序结果为：[1, 2, 3, 4, 5, 5, 6, 7, 9, 10]
# 4. 复杂度分析
【时间复杂度分析】
最优情况：每一次切分选择的基准数字刚好将当前序列等分
快速排序的一次切分从两头开始交替搜索，直到 i 和 j 重合，因此，一次切分算法的时间复杂度为O(n)，但整个快速排序的时间复杂度和切分的次数相关。把数组的切分看做是一个树，那么上图就是它的最优情况，共切分了logn次，所以，最优情况下快速排序的时间复杂度为O(nlogn)
最坏情况：每一次切分选择的基准数字是当前序列中最大数或者最小数
如由小到大排列9，8，7，6，5，4，这使得每次切分都会有一个子组，那么总共就得切分n次
所以，最坏情况下，快速排序的时间复杂度为O(n^2)
【空间复杂度分析】
空间复杂度就是在交换元素时那个临时变量所占的内存空间；
- 最优的空间复杂度：开始元素顺序已经排好了，空间复杂度为：0；
- 最差的空间复杂度：开始元素逆序，则空间复杂度为：O(n)；
平均时间复杂度：O(nlogn)
平均的空间复杂度为：O(1)