1. 堆的概念

Q：什么是堆？

堆分为大顶堆和小顶堆，大小顶堆都要满足的条件为：

大顶堆：

1. 是完全二叉树
2. 所有父节点的值大于子节点

根结点（亦称为堆顶）的关键字是堆里所有结点关键字中最大者，称为大根堆，又称最大堆（大顶堆）。

小顶堆：

1. 是完全二叉树
2. 所有父节点的值小于子节点

根结点（亦称为堆顶）的关键字是堆里所有结点关键字中最小者，称为小根堆，又称最小堆（小顶堆）。

此次堆排序我们用大顶堆来实现。

2. 堆排序思想

计算机是不知道堆这个结构的，堆是我们抽象出来的逻辑结构，它通常用数组来实现。

【堆排序过程】

1. 构造一个大顶堆，取堆顶数字（也就是最大值）

2. 再将剩下的数字构建一个大顶堆，取堆顶数字（也就是剩下值当中的最大值）

3. 重复以上操作，直到取完堆中的数字，最终得到一个有序的序列

关键就在于，我们怎么构造这个大顶堆？怎么往出取数字？

---

构建大顶堆

根据大顶堆的概念，我们知道首先它是一棵完全二叉树 (opens new window)

设树的深度为h，除了最后一层（第h层）外，其他各层的节点都达到最大个数。第h层所有的节点都连续集中在最左边

那么，我们首先把待排序的序列，按顺序（由上到下，从左到右）构建成为无序的完全二叉树

现在已经是一棵树了，我们再将完全二叉树构建为大顶堆

构建分为两步：

1. 由下至上扫描二叉树，检查当前节点是否都大于其左右孩子节点。

2. 如果当前节点小于左孩子节点或者又孩子节点，则和子节点交换位置

   如果当前节点都小于子节点，则和左孩子节点或者右孩子节点中较大的孩子交换。使交换后的父亲节点都大于左右孩子节点

---

3. 堆排序详解

【大顶堆构建详解】

我们先从右下角开始扫描：

没有右孩子则无须比较

然后再扫描左下角

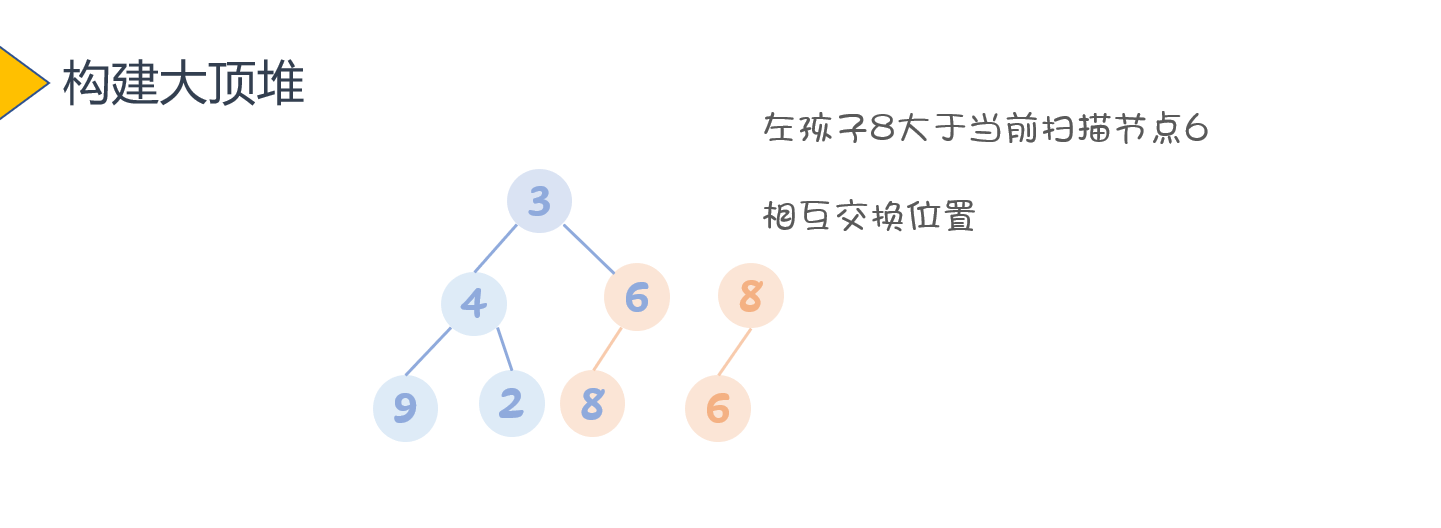
此时，后两层已经构建完成，我们再继续向上扫描

此时，我们发现当前节点（此时叫做堆顶），均小于他的左右孩子。我们只需要让堆顶和左右孩子中较大的交换位置即可。发现左孩子比右孩子大，则堆顶和左孩子交换位置

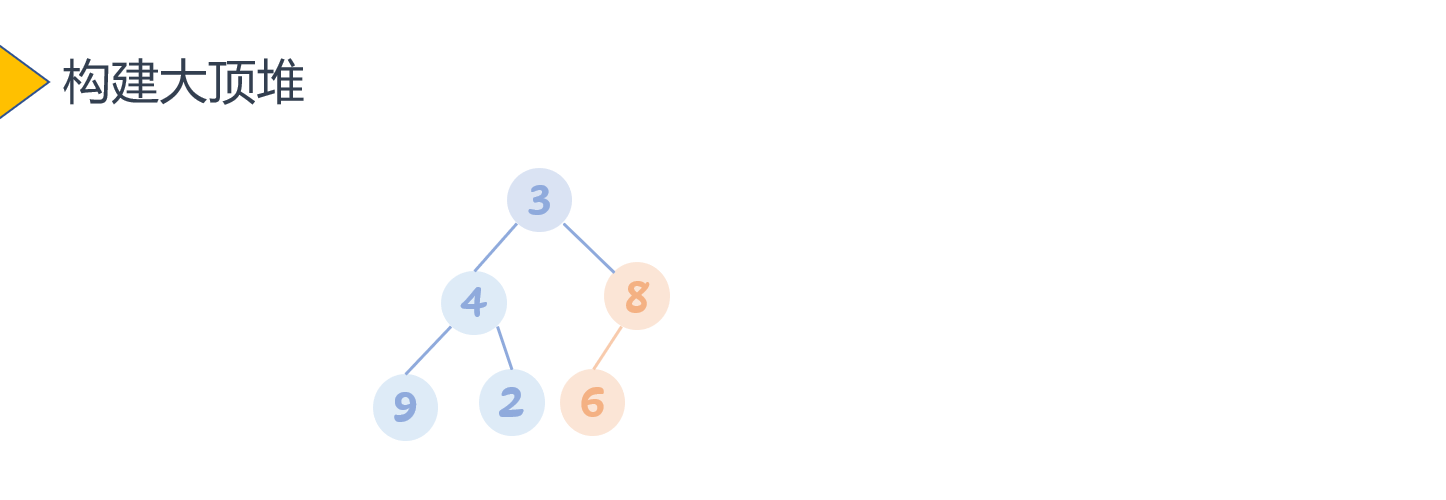
交换完成后，发现有点小问题了。

此时，交换完的子树是符合条件了。但是以3为父节点的子树又得需要调整了。

然后，我们继续重复上述构建过程

此时，符合条件的大顶堆构建完成

取数排序

构建完了大顶堆，我们最终的目的是要排序。那么，怎么往出取数字让序列变得有序呢？

此时，我们发现，大顶堆的堆顶是序列中最大的元素。换句话说，此时要排序的序列中的最大值找到了，我们把它拿出来：

将堆顶跟末尾的节点交换位置，经过自我调整，第2大的元素就会被交换上来，成为最大堆的新堆顶。

这里有个细节操作，就是砍断末尾元素

然后，此时又是一个新的完全二叉树去构建新的大顶堆：

继续重复此步骤：

这里9 和8位置放反了，改图比较麻烦，特此说明。

直到所有取出，二叉树没有节点，则排序完成。到此，堆排序结束

4. 代码实现

代码的思路是就是上面分析的过程，关键点都做了详细的备注

/**
 * @Author: Mr.Q
 * @Date: 2020-04-28 11:43
 * @Description:堆排序
 * data = {3, 4, 6, 9, 2, 8}
 */
public class HeapSort {

    /**
     * 堆排序
     * 1.构建堆 buildHeap()
     * 2.对堆进行排序 heapSort()
     * @param arr
     */
    public static void heapSort(int[] arr) {
        //先构建堆
        buildHeap(arr);
        //从末尾出发，开始排序
        for (int i = arr.length - 1; i >= 0; i--) {
            //交换堆顶和末尾节点(包含了砍断操作)
            swap(arr, i, 0);
            //数的节点数len是不断减少的(不断在砍断)，i代表当前数的节点个数； len == i
            heapify(arr, i, 0);
        }
    }

    /**
     * 构建大顶堆
     * @param arr
     */
    public static void buildHeap(int[] arr) {
        //该树的最后一个节点
        int last_node = arr.length - 1;
        //最后一个节点的父亲节点
        int parent = (last_node - 1) / 2;
        //自底向上对父亲节点做 hepify
        for (int i = parent; i >= 0; i--) {
            heapify(arr, arr.length, i);
        }
    }

    /**
     * 确保当前父节点大于左右子节点
     * @param data 待排序数组
     * @param len 树的节点个数

     * @param root 当前子树的根节点
     */
    public static void heapify(int[] data, int len, int root) {
        //递归的出口，当前根节点位置超出了树的范围

        if(root >= len) {
            return;
        }
        int left = root * 2 + 1; //左孩子

        int right = root * 2 + 2; //右孩子

        int max = root; //子树节点最大值

        //当前父节点有右孩子，并且父节点小于右子树
        if (right < len && data[max] < data[right]) {
            max = right;
        }
        //当前父节点有左孩子，并且父节点小于左子树
        if (left < len && data[max] < data[left]) {
            max = left;
        }
        //找到了当前子树的最大值，用最大值与其父亲节点交换
        if (max != root) { //如果父节点均大于左右孩子，则不用交换

            swap(data, max, root);
            //继续对其下面的子树构建
            heapify(data, len, max);
        }
    }

    /**
     * 交换数字
     * @param data
     * @param i
     * @param j
     */
    public static void swap(int[] data, int i, int j) {
        int temp = data[i];
        data[i] = data[j];
        data[j] = temp;
    }
}

hepify操作

1. 先构建堆buildHeap

2. 然后进行排序

5. 复杂度分析

• 时间复杂度：O(nlogn)

• 空间复杂度：O(1)